薙ぎ払いレーザーを改めて実装をする

昨日にこちらを大幅更新しました。

その更新の一部分であるボスの挙動、その中でボスのレーザの挙動の実装について見ていきたいと思います。

挙動の仕様

ボスのレーザはただ一方向に発射するのではなく、いわゆる薙ぎ払いを行うようにしています。

ラピュタのあれですね。

もう少し細かくやりたい挙動をまとめると

• 対象に向けてレーザーを放つ
• ただし、最初は角度をずらして放つ
• 対象地点にめがけて発射角を修正していく
• 対象地点を直線上に経由する
• 最終的にさらにずれてレーザーの発射を終える

結構量が多そうですが図示すると以下の通り

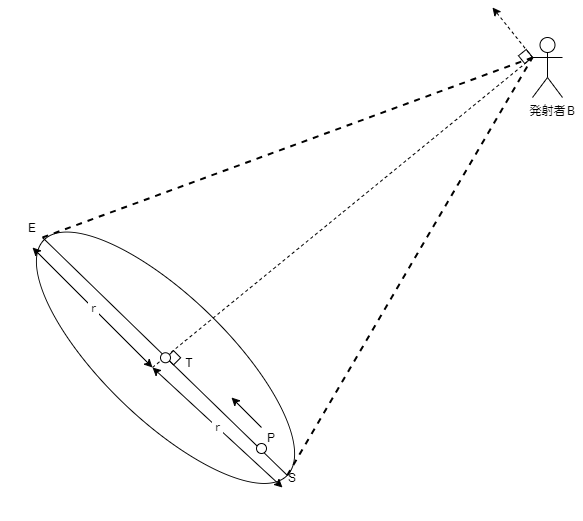
点S から 点E を移動する点Pを求める。

俗に言う点Pの問題ですね。

実際に実装していきたいと思います

実際に実装する

実際に 点P を求めるには、まず 点S と 点E を求める必要があります。

点Sと 点Eを求めるために外積を用います。

外積は以下の通りです。

必要な材料としては

• 発射者B と ターゲットT のベクトル

　Unity上で表すとこのようなものになりますね

var dir = T.transform.postion - B.transform.postion;

• Y軸方向のベクトル

　こちらはVector3で用意してくれています

var up = Vector3.up;

• ターゲットT からの距離ｒ

　こちらは予めインスペクターなどで定義しておきましょう

このように必要な材料は全て揃っていますね。

実際に計算してみましょう。

var dir = T.transform.postion - B.transform.postion;
var s   = Vector3.Cross(forward, Vector3.up).normalized * r;
var e   = -s;

これで 点Sと 点E が求められました。

引き続きここから点Pを求めましょう。

点P を求めるために 点Sと 点E を移動するのに必要な時間が必要です。

仮に t としてみましょう。

Vector3.Lerp(s, e, Time.deltaTime / t);

Vector3.Lerp は2つの点の間を補間する関数でまさに 点P を求めるために作られたもののため、時間が設定できればこの通りUnity上では1行で完結します。

これで必要な材料の点Pが求められました。

あとはここに弾を発射するなり、レーザを打つなりすれば薙ぎ払いの挙動が実装されます。

実物

実際の挙動はこちらになります。

以前バージョンからは大幅に変わり、しっかり薙ぎ払いが行われています。

まとめ

前回は割とそれっぽい挙動でまとまっていましたが

今回は薙ぎ払いの挙動を整理し、しっかりルールや法則に基づいた挙動になりました。

いくらUnityの標準機能で物理演算や数学の公式が用意されていますが

3Dの自作ゲームを作る場合には知識が必須なのでしっかり知識は蓄えていきましょう。

あとは公開中ですのでぜひプレイしてみてください。